Organizers: Francesco Bellucci (University of Bologna), Frederik Stjernfeldt (Aalborg University Copenhagen), and Ahti-Veikko Pietarinen (Hong Kong Baptist University)
Workshop Description
The phrase “philosophy of notation” was coined by Charles S. Peirce in 1885 to indicate the investigation of the principles that underlie all notations, diagrammatic and otherwise. Peirce was most interested in a wide range of algebraical and graphical notations for logic, but the phrase can also be applied to his studies on the types of numerical notations, and more generally to his research into formal languages for logic and mathematics and to the norms and principles of scientific notations and nomenclatures. As with its better-known term of “ethics of terminology”, Peirce also extensively wrote on the “ethics of notation” and its applications in science, pedagogy, and scientific communication.
Peirce’s philosophy of notation was largely based on his theory and classification of signs, or semiotics. Semiotics in Peirce is fundamentally a descriptive discipline: it determines which sign types are involved in establishing propositions and arguments, and how these signs relate and combine. The philosophy of notation, by contrast, involves a normative dimension: it determines which sign types should be used in constructing logical and mathematical notations, and how these signs should relate and combine.
Normative assessments, in turn, are based on aims. As far as logic is concerned, it is now sufficiently clear that the aim of Peirce’s investigations into, and experimentations with, logical notations was the achievement of a (nearly) perfectly analytical language, a language that would be an immediate and transparent instrument of logical analysis, or as he also sometimes says, a language that would provide an “icon of logical analysis”. Ethical considerations in notation choice and design are also involved: The person who introduces a conception into science has both the right and the duty of prescribing a terminology and a notation for it; and her/his terminology and notation should be both conservative and to be followed except where disadvantageous.
The workshop’s aim is to provide a forum for an organic and systematic discussion of Peirce’s philosophy of notation. It will cover topics such as the development of Peirce’s unique notations both algebraic and graphical, for both logic and mathematics; his idea of diagrammatic reasoning; his philosophy of mathematics and of mathematical practice; his principle of the “ethics of notation”; his general history and philosophy of science; and the reception, interpretation, and criticisms of his ideas about notations.
Keywords: Analysis in logic; Algebra of logic; Diagram; Diagrammatic reasoning; Ethics of notations; Iconicity; Logic; Logical graphs; Mathematical notations; Notations; Numerical notations; Terminology; Peirce.
Accepted talks
- Dave Beisecker: Peirce, Hegel, and Diagrams of Pure Being and Nought
- Francesco Bellucci: Linearity Lost
- Nathan Haydon and Ahti-Veikko Pietarinen: Ethics of Notation, Existential Graphs, and Logical Analysis
- Javier Legris: Note on the interpretation of the line of identity in the Beta Graphs
- Minghui Ma and Ahti-Veikko Pietarinen: Monadic Existential Graphs and their Notational Novelties
- Amirouche Moktefi: On the plurality of logical notations
- Jukka Nikulainen and Ahti-Veikko Pietarinen: Ethics and Philosophy of Notation in the egpeirce LaTeX Package
- Markus Pantsar: Peirce’s Philosophy of Notations and the Trade-offs in Numeral Symbol Systems
- Frederik Stjernfelt: A Note on an Invisible Notation
Abstracts
Peirce, Hegel, and Diagrams of Pure Being and Nought
Dave Beisecker (University of Nevada)
It is well-known that Peirce starts off his philosophical career reacting not only against Cartesianism, but also against Hegelian Logic. Especially egregious for Peirce was its ultimate equation of “pure being” with nothingness or “nought.” As early as 1868, Peirce contended that the proper understanding of being and nought lies in understanding the particular functions of their respective signs. By the time he came to develop the existential graphs, however, Peirce’s attitude toward Hegel had softened, indeed, to the point of even lauding Hegel “in some respects” as “the greatest philosopher that ever lived” (CP 1.524). Perhaps it should come as no surprise, then, that the major notational innovations of the existential graphs consist precisely in the development of signs for “being” and “nought” respectively (the spots, the connecting lines, and the ovals). While diagrams in chemistry might have provided a chief source of inspiration for Peirce’s logical graphs, that doesn’t rule out that there might have been other sources. That is especially so in thinking about the function of the cuts or ovals. There is some indication that Peirce himself thought of these signs in explicitly Hegelian terms (see, for instance, LOF 1: 67, LOF 1: 409, and LOF 3: 257). Accordingly, I propose to call graphs that lack any symbols representing empirical predicates of relations “graphs of pure being.” These would include graphs of quantity. As I will show, one can use these graphs to visualize some of the stages through which Hegel thought consciousness had to pass in order to come to increasingly adequate conceptions of being, including the idea that the conception of unity has to involve a negation of otherness (a negation of a negation) or “a return from self-alienation.” Peirce also seems to get this when he speaks (CP 1.491), with some approval, of Hegel’s “dilemmatic” method for tracing the true evolution of thought and telling us (CP 1.42) that his own philosophy “resuscitates Hegel, though in a strange costume.”
Linearity Lost
Francesco Bellucci (University of Bologna)
Natural language is linear. Linearity is the second of two characters that Saussure (1916) attributes to natural languages. We have to impose linear order on sounds and words when we speak: the sensory-motor system does not allow production in parallel. Human language phonotactics can be described in terms of linear constraints, which dictate which sounds must precede or follow which sounds. In spoken language the linear order is that of time; in written language the linear order is that of space, i.e. the line.
Linguists have long recognized that the syntactical structures of human languages combine the hierarchical structure with the linear arrangement. Lucien Tesnière (1959) was perhaps the first to lucidly point to the “antinomy” between linear order and hierarchical order. The linear order imposed on sounds and words hides the most important aspect of human language, i.e. the fact that syntactical relations, structures, and rules are hierarchical, not linear (Moro 2016; Chomsky 2019).
Human language syntax is hierarchical; linear ordering constraints are only due to the way language is externalized, i.e. are only due to the characters of the sensory-motor system (vocal tract). These characters may even have had a evolutionary history that is distinct and independent of the way human computational capacity has evolved (Berwick and Chomsky 2015). Syntax is based on hierarchical structures. It is only the way these structures are externalized that imposes linearization. Linearism is inseparable from phonologism
Like natural language, logical languages must, if they are expressive enough, represent hierarchical and recursive structures. Yet, unlike natural languages, logical languages are written but not spoken. While in the case of natural languages linearity is biologically determined by the nature of the sensory-motor system that governs its externalization, in the case of formal languages linearity is only a consequence of their imitating natural languages (Enderton 1970).
The present paper examines Peirce’s invention of non-linear languages for the representation of quantificational logic, languages that he generically termed “logical graphs”. The first version of the logical graphs is in some manuscripts of 1882. Although the 1882 “proto-graphs” (Bellucci and Pietarinen 2016; Bellucci and Pietarinen 2023) do not achieve the same expressive power as the later entitative and especially existential graphs, yet the fundamental properties of the graphs are already there.
The basic idea is the following. Certain equivalencies depending on symmetric relations or operations (like “A & B = B & A” or “No A is B = No B is A”) are a mere consequence of the linear nature of the syntax. Equivalencies like these only belong to the language, not to the object the language represents. In a non-linear language, no such equivalence can be expressed. One may put the matter thus: the linear vs non-linear divide only pertains to the external manifestation of the language, not to its deep structure; it is the external manifestation of the language that dictates what the language must express and what it can leave unexpressed. A linear language must order the unordered components of symmetric relations or operations, and thus is forced to express equivalencies of the sort just mentioned, while a non-linear language can leave order unexpressed. While linearity is lost, much is gained in notational simplicity and economy.
References
- Bellucci, F. and Pietarinen, A.-V. (2023). Existential Graphs: History and Interpretation. In: de Waal, C. (ed.) The Oxford Handbook of Charles S. Peirce, Oxford: Oxford University Press, 240–260.
- Bellucci, F. and Pietarinen, A.-V. (2026). “From Mitchell to Carus: Fourteen years of logical graphs in the making.Transactions of the Charles S. Peirce Society 52: 539–575.
- Berwick, R.C. and Chomsky, N. (2015). Why Only Us. Language and Evolution. Cambridge, MA: The MIT Press.
- Chomsky, N. (2019). The UCLA Lectures.
- Enderton, H.B. (1970). Finite partially ordered quantifiers. Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 16: 393–397.
- Moro, A. (2016). Impossible Languages. Cambridge, MA: The MIT Press.
- Saussure, F. (1916). Cours de linguistique générale. Paris: Payot.
- Tesnière, L. (1959). Éléments de syntaxe structurale. Paris: Klincksieck.
Ethics of Notation, Existential Graphs, and Logical Analysis
Nathan Haydon (Tallinn University of Technology) and Ahti-Veikko Pietarinen (Hong Kong Baptist University)
Peirce’s Existential Graphs (EGs) [3] owe their development to his commitment beyond algebraic study of relations: finding better logical notations. His aim was to describe a notation that is as analytic and as iconic as possible, where the logical signs are not only minimal in number and appearance but also maximally informative and reflect the very features they represent. Such is the continuous line – the line of identity – that integrates over several logical features of the verb for “being”: identity, existence (quantification), predication, and subsumption [6]. Another example is juxtaposition (conjunction) being the default connective absorbed by the sheet of assertion [1]. In addition to these “perfect” logical notations, Peirce worked with the ‘cut’ (“sep”, shading) as a separation from the sheet of assertion, and “the blot” as a notion of absurdity [7]. We can add the logical sign of “the scroll”—often considered by Peirce as the most primitive and most essential sign to represent inference in the graphs—which Peirce takes the scroll to iconize illations and inclusions.
From these, we move on to discuss two further notational forks in Peirce’s graphical journey. Recent work has emphasized Peirce’s flirtations in the direction of linear logic [2, 3, 8], showing he understood relative sum and residuation corresponding to the “par” and “linear implication” from linear logic. This leads us to analyze notational choices Peirce made for representing relative sum and residuation and their corresponding features in the diagrammatic syntax of EGs.
We end by addressing a riddle that Peirce encounters: the distinction between logical and mathematical provenance of analysis. He commonly remarks that the logician’s aim of logical analysis is, unlike the mathematician’s, to break reasoning down into its smallest discernible steps. He goes on to note that the smallest steps of reasoning are often not the most efficient means of representing the aims of mathematical reasoning and calculation at any one time. In contrast to this position, we often find applications of rules for EGs and the resulting derivations of theorems that are remarkably simple, often cutting through extraneous ‘mathematical’ steps [4]. (For certain classes of problems, the length of proofs by EG rules of transformations take a square root from the length of proofs by natural deduction, for example.) We argue that Peirce’s concern for notation allows the graphical method to represent reasoning both in its smallest and simplest (iconic) steps, which could mean that good diagrammatic syntax embeds intrinsic properties that bring the two measures of complexity, analytic and computational, together, to meet both logical and mathematical purposes, highlighting the role and importance of Peirce’s maxim of the ethics of notation [5].
References
[1] Bellucci, F., Chiffi, D. and Pietarinen, A.-V. (2021). Assertion, Conjunction and Other Signs of Logic: A Contribution to the Philosophy of Notation. Transactions of the Charles S. Peirce Society: A Quarterly Journal in American Philosophy 57(2), pp. 270–287.
[2] Haydon, N. (2023). C.S. Peirce’s Early Developments in Linear Logic. Currently under review.
[3] Haydon, N. and Pietarinen, A.-V. (2021). Residuation in existential graphs. In Basu, A., Stapleton, G., Linker, S., Legg, C., Manalo, E., and Viana, P., eds., Diagrammatic Representation and Inference, pp. 229–237, Cham. Springer.
[4] Ma, M. and Pietarinen, A.-V. (2016). Proof Analysis of Peirce’s Alpha System of Graphs. Studia Logica 105(3), pp. 625–647.
[5] Peirce, Charles S. Logic of the Future : Writings on Existential Graphs. Ed. by A.-V. Pietarinen. Vol. 1: History and Applications. Vol. 2/1: The Logical Tracts. Vol. 2/2: The 1903 Lowell Lectures. Vol. 3/1: Pragmaticism. Vol. 3/2: Correspondence. Boston & Berlin: De Gruyter, 2019-2024.
[6] Pietarinen, A.-V. (2006). Signs of Logic: Peircean Themes in the Philosophy of Language, Games, and Communication. Synthese Library 329. Dordrecht: Springer.
[7] Pietarinen, A.-V., Bellucci, F., Bobrova, A., Hayden, N. and Shafiei, M. (2020). The Blot. In Pietarinen, A.-V. et al. (eds.), Diagrammatic Representation and Inference. Lecture Notes in Computer Science 12169, Springer.
[8] Pratt, V. R. Origins of the Calculus of Binary Relations. In International Symposium on Mathematical Foundations of Computer Science, pp. 142–155. Springer, 1992.
Note on the interpretation of the line of identity in the Beta Graphs
Javier Legris (University of Buenos Aires)
Identity was a key notion in the origins of symbolic logic. Boole and the succeeding tradition in the algebra of logic formulated logical laws as equations. It was indispensable for constructing proofs in Frege’s Begriffsschrift and in Peano’s axiomatic system for arithmetic. Charles S. Peirce included identity in his algebraic system for predicate logic, developed in his seminal paper published in 1885; not only the principle of substitution but also the (higher-order) principle of indiscernibles.
Later, in the context of his diagrammatic system of Existential Graphs, Peirce introduced identity by means of the line of identity, the basic sign of the Beta System. According to the mainstream interpretation of EG (originated by Zeman in 1964 and Roberts in 1973), it fulfills the roles of the individual variables, the existential quantifier, and the identity of predicate logic with identity. Through the line of identity and the cut, the classical universal quantifier can be defined.
The analytic function of the logical signs of EG is philosophically the most prominent. The purpose of EG was “to dissect the operations of inference into as many steps as possible” (Peirce CP 4.424). According to Peirce, analysis meant the decomposition of something into its basic elements. It applied above all to signs in general (see, inter alia, CP 1.294). Hence, the line of identity should be an unanalyzable sign, suggesting that the notions of existence and identity are expressed by the same sign.
This contribution is a follow-up to my paper, Legris 2021. Its aim is to show that the line of identity does not express exactly what is understood as identity in Classical Predicate Logic with Identity. This fact was already suggested (see, e.g., Pietarinen’s introduction to Peirce’s LoF), but it was not sufficiently emphasized.
In order to justify this claim, some cases will be taken into account. For example, the principle of substitution corresponds to the graph
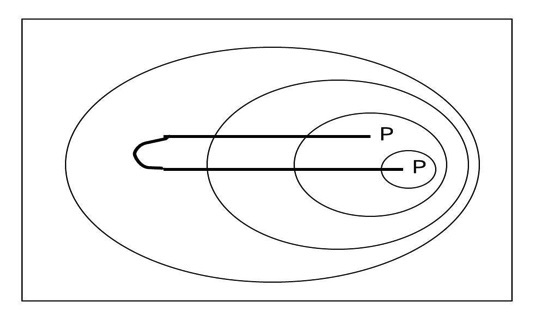
in the Beta system. Its meaning is not clear. In the notations developed for symbolic logic, the main function of the sign of identity was to express the substitutivity of individual terms (indispensable in proofs). In a notation lacking a set of individual terms, like EG (at least in the standard presentation), there is no need for such substitutivity. Another case is definite descriptions, which are clearly expressed in the Language of Predicate Logic with Identity but not in the Beta System
References
- Legris, J. 2021. On Identity in Peirce’s Beta Graphs. In: Basu, A., Stapleton, G., Linker, S., Legg, C., Manalo, E., Viana, P. (eds) Diagrammatic Representation and Inference. Diagrams 2021. Lecture Notes in Computer Science, vol 12909. Springer, Cham. https://doi.org/10.1007/978-3-030-86062-2_22
- Peirce, C. S. CP. Collected Papers. 8 volumes, vols. 1- 6 ed. by Charles Hartshorne & Paul Weiss, vols. 7-8 ed. by Arthur W. Burks. Cambridge (Mass.), Harvard University Press, 1931-1958.
- Peirce, C. S. LoF. Logic of the Future, vols 1-2 ed. by Ahti-Veikko Pietarinen. Berlin, Boston: De Gruyter, 2021 – 2022.
- Roberts, D., 1973, The Existential Graphs of Charles. S. Peirce. La Haya, Mouton, 1973.
- Zeman, J. J. 1964. The Graphical Logic of C. S. Peirce, Ph.D. thesis, University of Chicago.
Monadic Existential Graphs and their Notational Novelties
Minghui Ma (Sun Yat-Sen University) and Ahti-Veikko Pietarinen (Hong Kong Baptist University)
Peirce’s theory of existential graphs (cf. e.g. [1]) consists of at least three parts. The graphs are scripted on the sheet of assertion (SA) from atomic graphs using logical devices. The alpha part treat with Boolean algebras and the alpha system is a graphical calculus for the classical propositional logic (cf. [6, 7, 9]). A variant of the alpha system gives rise to a graphical deep inference system for intuitionistic propositional logic (cf. [10]). In the present work, we introduce a beta graph system for the monadic fragment of first-order logic (without identity).
A beta graph is built from predicates using the cut (ovals) and the continuous heavy line of identity. One problem for developing a graphical system for the first-order logic is that we need primitive graphs of n-nary predicates (rhemas, spots) for each n≥1. In general, we write a predicate on the SA, with n-hooks at the periphery of the graphical representation of the predicate provided in some designated order (LoF 1; [3, 4]). Moreover, no single predicate term with n-hooks unoccupied with the lines is scriptible on the SA since such incomplete predicates certainly have no assertible content. Thus, in this paper we restrict the system to monadic predicates which only have one hook at any location of the periphery. This leads to a graphical system for the monadic first-order logic.
Halmos [5] proposed monadic Boolean algebras as the algebraic structures for the monadic first-order logic. A monadic Boolean algebra is an algebra (B, ∃) where B is a Boolean algebra and ∃ is a unary operation on B such that ∃0 = 0,
x ≤ ∃x and ∃(x ∧ ∃y) = ∃x ∧ ∃y for all x, y ∈ B. Peirce’s methodology of developing logical graphs was to discover an instrument of reasoning about logical algebras. We give a systematic construction of monadic existential graphs using the SA, unary predicates, and n-branching line of identity where n ≥ 1. Then, we develop a graphical system GM based on the alpha system ([6]) by adding the lines of identity. We prove that GM is characterized by the variety of all monadic Boolean algebras. The system GM has the finite (algebraic) model property and is decidable.
From the perspective of the philosophy of notation, GM has interesting features and implications. Among them is that an unattached line on the SA and SA are identical. Peirce notices how the SA is a graph “already bearing a proposition” (R S-30, 1906; LoF 3/1: 245) and how attachments in the modal-logic case considered by Peirce may be made “to a hook of the cut” (R S-31, 1903; LoF 2/2: 264; [8]).
Monadic existential graphs (MEG) bring these observations out particularly well. Zero-place constants (the top and bottom elements in the algebra) are imagined in their graphical correlates to have ‘hooks’. Cuts with lines attached to them are closure-algebraic operators with S5 system of modal logic as the model of GM. In a sense, imposing quantifiers on a Boolean algebra implicates that there in fact is a vanishing distinction between the alpha and beta systems of existential graphs.
We also consider the case of extending GM to a notation in which the line is to have direction, to preserve intended readings of certain natural-language sentences in which ordering of predicates matters. This can be implemented in alternative notational ways: either with directed lines, or in the modification of the point of teridentity of the branching line, or as a metalogical rule e.g. in the sense of Peirce’s “Gamma expression of Beta graphs” (LoF 2/2: 270), where the direction of lines is expressed at the metalinguistic (metagraphical) level of the Gamma graphs.
References
[1] D. Robert. The Existential Graphs of Charles S. Peirce. The Hague, Paris: Mouton, 1973.
[2] G. Bezhanishvili. Varieties of monadic Heyting algebras. I. Studia Logica 61(3): 367–402, 1998.
[3] R. Atkins. On Three Levels of Abstractness in Peirce’s Beta Graphs. History and Philosophy of Logic, 44, 16–32, 2023 10.1080/01445340.2022.2056781
[4] F. Bellucci, A.-V. Pietarinen. Existential Graphs as an Instrument of Logical Analysis. Part 1: Alpha. The Review of Symbolic Logic, 9(2), 209–237, 2016 10.1017/S1755020315000362
[5] P. Halmos. Algebraic logic I. Monadic boolean algebras. Compositio Mathematica 12, 217–249, 1954–1956.
[6] M. Ma and A.-V. Pietarinen. Proof analysis of Peirce’s alpha system of graphs. Studia Logica 105, 625–647, 2017.
[7] M. Ma and A.-V. Pietarinen. Peirce’s calculi for classical propositional logic. The Review of Symbolic Logic 13(3), 509–540, 2020.
[8] M. Ma and A.-V. Pietarinen. Gamma graphical calculi for modal logics. Synthese 195, 3621–3650, 2018.
[9] M. Ma. Peirce’s logical graphs for Boolean algebras and distributive lattices. Transactions of the Charles S. Peirce Society 54(3), 320–340, 2018.
[10] M. Ma and A.-V. Pietarinen. A graphical deep inference system for intuitionistic logic. Logique et Analyse 245, 73–114, 2019.
[11] C.S. Peirce. Logic of the Future. Writings on Existential Graphs. A.-V. Pietarinen (ed.). Three volumes in five books. Berlin & Boston: De Gruyter. (LoF)
On the plurality of logical notations
Amirouche Moktefi (Tallinn University of Technology)
Charles S. Peirce is a major actor in the development of modern logic (Bellucci & Pietarinen 2015). In his time, a multitude of symbolic and diagrammatic notations were proposed to express logical entities and propositions. This plurality led to a friendly competition among logicians in their quest for better notations to tackle logical problems. For the purpose, logicians commonly compared their solutions in print (Moktefi 2019). In this setting, some logicians drafted tentative guidelines for the design of new notations. Others called for a “slight social repression” against new proposals (Venn 1881).
We consider the place of Peirce’s philosophy of notation within this context (Peirce 1885). In particular, we consider what the work of Peirce’s logic students teaches us in this respect. It is, indeed, somewhat puzzling that Peirce’s students, especially Christine Ladd-Franklin and Oscar H. Mitchell, introduced their own notations and competed against their teacher (Peirce 1883). We discuss the extent to which this permissive attitude towards the plurality of logical notations aligns with Peirce’s ethics of notation. Indeed, Peirce’s principle seems to rather discourage new notations unless older ones “prove positively and seriously disadvantageous to the progress of science”. Finally, we outline some important differences between Peirce’s school and those of George Boole and Giuseppe Peano regarding the plurality of logical notations.
References
- Bellucci, F., Pietarinen, A.-V. (2015), ‘Charles Sanders Peirce: Logic’, Internet Encyclopedia of Philosophy, https://iep.utm.edu/peir-log/
- Moktefi, A. (2019), ‘The social shaping of modern logic’, in D. Gabbay et al. (eds.), Natural Arguments: A Tribute to John Woods, London: College Publications, 503-520.
- Peirce, C. S., ed. (1883), Studies in Logic by Members of the Johns Hopkins University, Boston: Little, Brown, and Co.
- Peirce, C. S. (1885), ‘On the algebra of logic. A contribution to the philosophy of notation’, American Journal of Mathematics, 7, 197–202
- Venn, J. (1881), Symbolic Logic, London: Macmillan.
Ethics and Philosophy of Notation in the egpeirce LaTeX Package
Jukka Nikulainen (University of Helsinki) and Ahti-Veikko Pietarinen (Hong Kong Baptist University)
One of the biggest obstacles in advancing Peirce’s non-standard and unconventional notations and his multiple diagrammatic systems of logical representation and reasoning has been the lack of established standards, tools, and methods for neatly representing these notations and their ‘visual’ elements on a page in a uniform fashion. Here we demonstrate the content and workings of the LaTeX package, egpeirce, released in 2023 with documentation [1, 2: LoF], which was precisely developed for to assist in transcribing thousands of pages rife with logical graphs and other atypical notations. The package unifies, automatizes, and standardizes the design, drawing, and communicating Peirce’s myriad notations for logic and algebra.
We review the specifications and show the full list of Peirce’s notations now available in LaTeX, illustrating that they accord with Peirce’s own manifold descriptions, explanations, and demands about them as expressed in his manuscript writings and letters to the editors concerning what his notations were meant to achieve and how they should be treated, used, typeset, printed, cultivated, and handled editorially and otherwise. We showcase how the package developed during the editorial toil that went into the five books of the Logic of the Future series (Pietarinen 2019-2024, [2: LoF]), highlighting the problems and proposed solutions to countless notational, typesetting, and editorial demands originating from Peirce that had to be encountered during the two decades of work on these volumes. We then set the editorial work within the context of Peirce’s ethics and philosophy of notation [2: LoF 1]; a close parallel to how textual elements should be handled as comes clear from Peirce’s better-known writings on the ethics of terminology.
We argue that much of the last century’s failures to comprehend the totality of Peirce’s scientific and creative compositional output has been the failure to apply the ethics of notation and terminology to his own corpus, with subsequent temptations to eliminate large swaths of versions, fragments, worksheets and passages that glue the mind behind them together. With egpeirce LaTeX package at our disposal, we hope to dispel these scare-factors – both scholarly and public – from what might look like non-standard, deviant or disposable euphemistic notations but which in reality are congenial part of Peirce’s well-conceived attempt to set the course for future logical investigation and to steer clear from misconceptions of what logical languages can communicate us about meanings. Importantly, those goals included the pedagogies for public understanding of logic and reasoning (critical thinking, [3: LoF 2/2]).
References
[1] Nikulainen, J. (2023). Documentation for the egpeirce LaTeX package. The LaTeX Project Public License 1.3. https://ctan.org/pkg/egpeirce?lang=en
[2] Peirce, Charles S. (2019-2024). Logic of the Future: Writings on Existential Graphs. Ed. by A.-V. Pietarinen. Vol. 1: History and Applications. Vol. 2/1: The Logical Tracts. Vol. 2/2: The 1903 Lowell Lectures. Vol. 3/1: Pragmaticism. Vol. 3/2: Correspondence. Boston & Berlin: De Gruyter. (LoF)
Peirce’s Philosophy of Notations and the Trade-offs in Numeral Symbol Systems
Markus Pantsar (RWTH Aachen University)
In this talk, we connect two research directions concerning numeral symbol systems and their epistemological significance. The first direction concerns the cognitive processes involved in acquiring and applying different numeral symbols, e.g. the Indo-Arabic or Roman numeral systems. The second direction is a semiotic one, with focus on Charles Peirce’s Philosophy of Notation. Peirce’s work on logical formalism is famous, but less known are his ideas on numeral systems. Here we take Peirce’s considerations on central notions like iconicity and simplicity and examine their relevance for comparing different numeral symbol systems, in light of modern understanding of numerical and arithmetical cognition.
We argue that that simplicity and iconicity, for example, cannot be understood as single, uniform notions. Instead, they should be connected to different aims of numeral symbols that different systems fulfil to different degrees. The Indo-Arabic base-10 numeral system, for example, lends itself well for arithmetical calculations with pen and paper, but it comes with the price of a memorizing extensive addition and multiplication tables, which are known to cause problems for children in learning arithmetic. The Roman numeral system, on the other hand, has much smaller addition and multiplication tables, but it loses important characteristics of the Indo-Arabic system (such as the amount of symbols already expressing the magnitude of the number).
Through this type of analysis, we focus on the kind of trade-offs that different symbol systems imply in grasping and applying numeral symbols. We propose a list of cognitive, pragmatic, and communicative aims for numeral symbol systems, and present examples of different systems (Indo-Arabic, Roman, tallying) in terms of them meeting the aims.
A Note on an Invisible Notation
Frederik Stjernfelt (Aalborg University Copenhagen)
It is well known that when Peirce in the 1890s began his development of the “Existential Graphs” he picked, for the Alpha version of the EGs formalizing propositional logic, the very simple convention that placing two propositions side by side expressed their conjunction, one of the two defining conventions, along with the enclosure for negation or the double enclosure for implication. And, of course, these two conventions are inherited by the predicate logic of the Beta Graphs and the different sketches to further extensions of the Gamma Graphs. A bit earlier, he had attempted the converse convention in the aborted first version called “Entitative Graphs” where juxtaposition of two propositions should rather be interpreted as their disjunction. As it is well known that disjunction and conjunction are definable in terms of each other, it might seem a trivial discussion which one to prefer. Not so for Peirce who argued that it was more natural and iconic that AB meant “A and B” than “A or B”. This naturalness of the “invisible” notation of simple juxtaposition to mean conjunction seems to have two rather different roots: algebra and signs in the wild. This paper seeks to elucidate these two roots.
- Boole, George (1854). The Laws of Thought, London: Walton and Maberly
- Cajori, Florian (2013). A History of Mathematical Notations, N.Y.: Dover Publications.
- Pietarinen, A. and Stjernfelt F. 2023 “Semiotics in Mathematics and Logic“, in Bloomsbury Semiotics. Pelkey, J. (eed.). Bloomsbury Academic, vol.2, 13-34.
- Stjernfelt, F (2022). “Sheets in the Wild” and “Co-Localization as the Syntax of Multimodal Propositions” (chs. 6 and 5 of Sheets, Diagrams, and Realism in Peirce, Berlin: De Gruyter)
About the organizers
Francesco Bellucci is Associate Professor of Philosophy and Theory of Language at the University of Bologna. He is the author of Peirce’s Speculative Grammar (Routledge 2017), Signs and Demonstrations from Aristotle to Radulphus Brito (with C. Marmo, Brill 2023) and the editor of Charles S. Peirce. Selected Writings on Semiotics (De Gruyter 2020).
Frederik Stjernfelt is Full Professor of Semiotics, Intellectual History, and Philosophy of Science at Aalborg University Copenhagen. He is the author of Diagrammatology (Springer 2007), Natural Propositions (Docent Press 2014), and Sheets, Diagrams, and Realism in Peirce (De Gruyter 2022).
Ahti-Veikko Pietarinen is Professor of Philosophy at Hong Kong Baptist University, Department of Religion and Philosophy, and associate of Ethical and Theoretical AI Lab and the Centre for Applied Ethics. He is editor of the five-volume series Logic of the Future: Peirce’s Writings on Existential Graphs (De Gruyter 2019–2024).